Are you in a calculus/trigonometry class, or planning to join one? If the answer is “yes,” it is prudent to understand and be able to use the unit circle. That is one of the most important mathematical tools for helping you to easily solve for cosine, sine, or tangent of an angle. But how does the unit circle work?
Table of Contents
The definition of trigonometric ratios operates within the limits of right angles. If you take the three interior angles of a triangle (right triangle), they always sum up to 180º. Besides, since one of the angles measures 90º, the remaining two must be acute. Using this information about the right triangle, it is possible to define the cosine, sine, and tangent ratios for any angle.
The unit circle is considered the simplest way to solve for these ratios. In this guide, we will dig deeper into the unit circle to establish what it is, how it works, how to remember, and how to use unit circle to solve trig problems.
Closer Look At The Unit Circle
A unit circle (trig circle) is any circle whose radius is one. That also implies that the diameter of the circle is two (diameter is always double the length of the radius). Then, the center is the point where y-axis and x-axis intersect. See the image below.
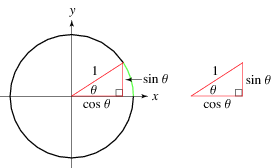
Figure i: The unit circle presentation showing the radius and right triangle
The unit circle makes it possible to easily calculate the sine, cosine, or tangent of angles that fall between 0° and 360°. From the above diagram (Figure 1), you can note that drawing a radius at any angle will create a right triangle.
If you take a closer look at the triangle, sine is the y-coordinate (vertical line), and cosine is the x-coordinate (horizontal line). Also, you can see the triangle’s radius becomes the hypotenuse.
At this point, we know that you can use the Pythagoras theorem (
) when solving for lengths of any side of a triangle (where a and b represent the lengths of the triangle while c is the hypotenuse). From the above equation, we can easily get the formula for right triangles in a unit circle.
Because we already know that 
we can simplify our equation like this: 
Now, we can go ahead and calculate the main angles in degrees and radians in the unit circle. Have a look:
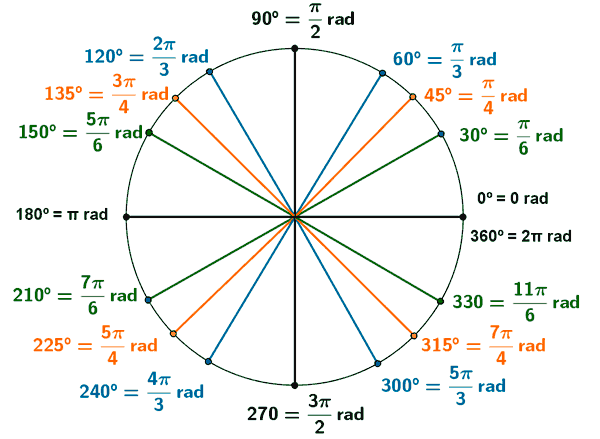
Figure ii: Demonstrations of angles in degrees and radians in a unit circle
At this point, one question that you might want to ask is: “What about when you only have a straight line (no triangle is formed)?” In this case, y-coordinate (sin 0°) will be zero while x-coordinate (cos 0°) will be one.
Application Of The Unit Circle – Why You Should Grasp It?
Looking at the application of the unit circle, perhaps you might be wondering: “How is this important?” There are a number of advantages why you should grasp the concept:
- The main advantage of the unit circle is that it allows you to solve for cosine, tangent, and cosine of any radian or degree. That is very important, especially in your mathematics and physics classes. You will also find it useful in applied sciences such as geography and chemistry. Thus, you need to grasp it to pass most subjects that require some direct or indirect application of trigonometry.
- The unit circle helps to simplify learning mathematics without having to memorize a lot of concepts. In most of the cases, students are required to memorize over 15 angles as well as their values to correctly get the cosine, sine, and tangent of angles. But they do not need to memorize all of these when using the unit circle. They simply need to conceptualize its application.
- Unlike other subjects, trigonometry is a broad subject. In real life, you will need it in careers such as construction, aerodynamics, shooting, and engineering. Because the unit circle makes understanding trigonometry and mathematics easy, it is an important lever for student’s success.
How To Use The Unit Circle – Solving Problems With Trigonometry Circle
To effectively apply the unit circle for solving trig problems, it is important to take a closer look at the unit circle chart.
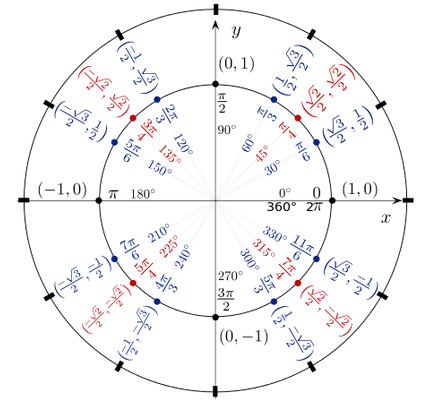
Figure iii: A detailed unit circle chart
If you can understand how the chart operates before starting the calculus class, you will find the subject relatively simple. To demonstrate how it works, take a look at the problem below. Note that in most of the cases, you will not be allowed to use a calculator.
- Solve: Sin 30°
To solve the problem, there is no need to get overwhelmed. Simply go back to the unit circle. You will find that the y-coordinate value is ½ at 30°. Because y-coordinate equals sine, we can easily calculate the answer as follows: Sin 30° =1/2.
- Solve:
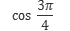
Using the unit circle, get the cosine (x-coordinate) for the problem. In this case, it is
. But how would the answer look like? Take a look:
It is pretty straightforward!
Special Tips To Remember And Apply The Unit Circle Trig
When you are faced with a trig problem, the unit circle is no doubt the simpler and straightforward method to apply compared to others. But hold on! You will not be provided by the chart that’s in Figure iii.
So, how do you memorize unit circle chart?
To help you remember the unit circle chart and apply it correctly, here are some useful tips:
- Focus On The Common Angles And Their Coordinates: To use the unit circle correctly, make sure to have the common angles at your fingertips. This means mastering their radians and degree and their coordinates. The moment you are able to get the common coordinates correctly, it will become easy to know other angles that fall between them.
- Make Sure To Grasp What Is Negative And Positive: in order to solve any trigonometric problem, it is crucial to know which y-coordinates and x-coordinates are negative. At this point, you need to apprehend that for a coordinate to be positive or negative; it depends on which quadrant it falls in. See the diagram below:
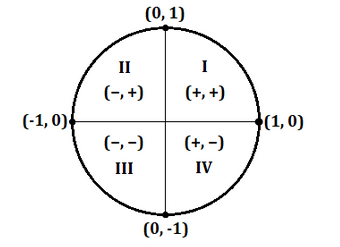
Figure iv: The unit circle showing the four quadrants
X-coordinate (cosine) will always be positive in quadrant I and IV but negative in quadrant II and III. However, y-coordinate (sine) will always be positive in quadrant I and II but negative in quadrant III and IV.
- Learn How To Solve For Tangent: to get it right on using the unit circle, you need to be enthusiastic about it. You should particularly focus on solving for tangent because it also makes it easy to know the values for cosine and sine. See the formula for tangent below:
Feel Free To Ask For Help
If you have interest in trigonometry, plan to join a trigonometry class, or a mathematics-based subject, understanding how to use the unit circle is very important. Although trigonometry is considered complex, the unit circle can help to make it simple and fun. This post has demonstrated how you can apply the unit circle and master it to solve your trig problems. However, if you still find it difficult to cope with your math homework, don’t be alarmed! Our professional writing service is always here to help you.
