Some math problems, such as Collatz Conjecture and the Riemann Hypothesis are brutally difficult. But this does not mean they cannot be solved. Your ability to effectively solve problems, even the hard math equations you thought were impossible, is having the right attitude. Then, use the right formula to get the correct answer.

Table of Contents
So, how good are you in SAT (standard admission test) math? Many students like preparing for the toughest questions they will come across on SAT to be more confident on the test day. We have gathered a few of the hardest math problems on SAT, along with answers and demonstrated how to solve them. If you understand these hard math problems, it will be a great step towards perfecting your preparation for SAT and later in your mathematics, physics, or engineering classes.
A Closer Look at SAT Math Sections
When working on SAT, the third and fourth parts are dedicated to mathematics. The math part has 54 mathematics questions: 10 student-produced response questions and 44 multiple-choice questions.
The ten multiple-choice questions require students to workout math problems and select answers from the choices provided. But the student-produced response questions are some of the most hard math questions because students have to calculate the right answers: there are no answer choices.
Notably, the SAT math questions are drawn from four main mathematics areas: algebra and functions; number and operations; data analysis, probability, and statistics; and geometry and measurements.
Therefore, you better be well prepared in all of the areas if you want to pass and join college.
Two Hardest Math Problems
Here, we have pooled the top two really hard math problems that many students find hard to crack. But even if each of them is a really hard math problem, we have cracked it and demonstrated how you should go about it. So, go ahead and practice until you can hack the questions like a pro.
- Question Two: Calculator is allowed
- We can get the point of intersection to know the optimal value of band then solve using the substitution method. This will give us the inequality below:
- Now, we move the variables to one side by adding 15x to each side. 20x≤3000.
- Then, divide each side using 20 to find x. x≤150. In Most cases, most students stop here. But we will move on to solve for coordinate b in (a,b). Simply call it the y-value.
- We will plug the x into each equation to get the value for b. We selected the second because it is simper: 5*150=750. There we go!
- Question Two: Calculator Not Allowed

This problem is a type of systems of linear inequalities in algebra. Here is how to solve it.
In the question, coordinates (a,b) lie in the solution set of these equations, and we want to determine the maximum possible value. Using inequalities, the graph will be shaded so that it includes a set of different values that must satisfy the inequality, therefore (a,b) lies in the overlapping section. Since it is a grid-in response (where only real numbers can be answers for the grip-in questions – you do not have options to simmer in infinity, right?). Further, we know one thing; the value of b has to be limited by intersection point.
Because the inequalities are either less than or equal to, we know that the point of intersection and the lines are part of the solution set. If only less or greater than symbols were there, the lines would not be part of the solution set. What does this imply?
5x≤−15x+3000, where x is equivalent to a, and the y-value equivalent to b.
![]()
The equation above shows how temperature F, measured in degrees Fahrenheit, relates to a temperature C, measured in degrees Celsius. Based on the equation, which of the following must be true?
- A temperature increase of 1 degree Fahrenheit is equivalent to a temperature increase of 59 degree Celsius.
- A temperature increase of 1 degree Celsius is equivalent to a temperature increase of 1.8 degrees Fahrenheit.
- A temperature increase of 59 degree Fahrenheit is equivalent to a temperature increase of 1 degree Celsius
A) I only
B) II only
C) III only
D) I and II only
Here is how to solve the problem:
Consider the equation as the common equation for a line.
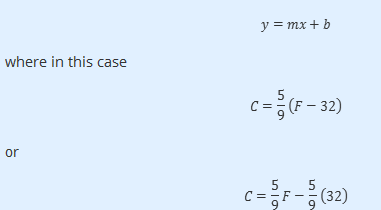
Can you see the slope of the graph? It is 5/9, which implies that for every rise in one degree F, the rise is 5/9 of one degree C.
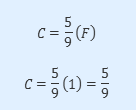
Therefore, it means that statement I is indeed true. This is the same as saying that when you increase one degree C you are raising 9/5 degrees F.
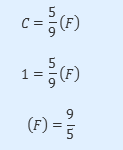
Because 9/5=1.8, it also implies that statement II is also true.
In the answers provided, the only option that has both statement II and I as correctly demonstrated is D. Note that you can also substitute further to check whether the other two options are actually wrong.
Your Questions on the Really Hard Math Problem Answered
Now that you have known the hard math equations and how to solve them, it is time to get down with a pen and paper. But we must indicate that many are the times when students feel inadequate to face challenging math problems fearing they will fail. Well, you should not stay with the problem. Whether it is the hardest algebra problem for 10th graders, for 9th graders, or for 7th graders, the best solution is seeking math professional help. The assistance is provided by professionals who are ready to help you with every math problem. To them, there are no hard math equations in the World.
What is the hardest math problem?
The Collatz Conjecture below is one of the hardest math problems out there.
It is in the mathematics discipline referred to as Dynamic Systems where situations change over time in semi-predictable ways.
What are the 7 hardest math problems?
- The Collatz Conjecture.
- Goldbach’s Conjecture.
- The Twin Prime Conjecture.
- The Riemann Hypothesis.
- The Birch and Swinnerton-Dyer Conjecture.
- The Kissing Number Problem.
- The Unknotting Problem.
Why do people say math hard?
- It takes time and energy.
- Teachers associate math with hard math riddles from an early age.
- You cannot get it right unless you have the right attitude.
- Some methods of teaching make it hard for people to grasp math concepts.
- Poor connection between math as a subject and students.
- They hear people saying it is difficult.
- Most concepts, unlike in other subjects, are abstract and require great imagination.




